Let’s say that you’re in Algebra 2 class and you’ve just been asked to find the approximate value of a logarithm – say, log₇(5). You’re told you’re allowed to use a calculator. Confident, you look for the “log7” key on your calculator… but you don’t find it. That’s because it doesn’t exist (at least on most calculators). What you will find, however, are the “log” and “ln” keys – and nothing else. But how can you be able to evaluate the logarithm, then, if there is no log7 key? The “log” and “ln” keys won’t work because those logarithms don’t have the same base. What do you do?

To solve this and countless other “evaluate-this-logarithm” problems, we can make use of a very handy tool – the Change of Base Formula.

In this lesson, we’re going to look at how to specifically use the formula to evaluate any logarithm. Any.

Ready to dive in?

The first step in evaluating any logarithm is to use the Change of Base Formula to rewrite the logarithm with a new base. Specifically, we’ll be rewriting all logarithms using a base of 10 or e (either works because both types of logarithms are present on all calculators).

To do this, we’ll need to recall the Change of Base Formula.

The formula states that:

log_ba = (log_ca)/(log_cb)

As you can see, we took a single logarithm with a base of b and a parameter of a, and we rewrote it as a quotient of two logarithms. The logarithm in the numerator takes a (the parameter of the original logarithm) as its parameter, and the logarithm in the denominator takes b (the base of the original logarithm) as its parameter. Both logarithms in the quotient have a new base of c – and c can be anything we want it to be, including 10 or e.

An important note when using the Formula is that the logarithm in the numerator always takes in the parameter of the original logarithm, and the logarithm in the denominator always takes in the base of the original logarithm – you can’t swap the order.

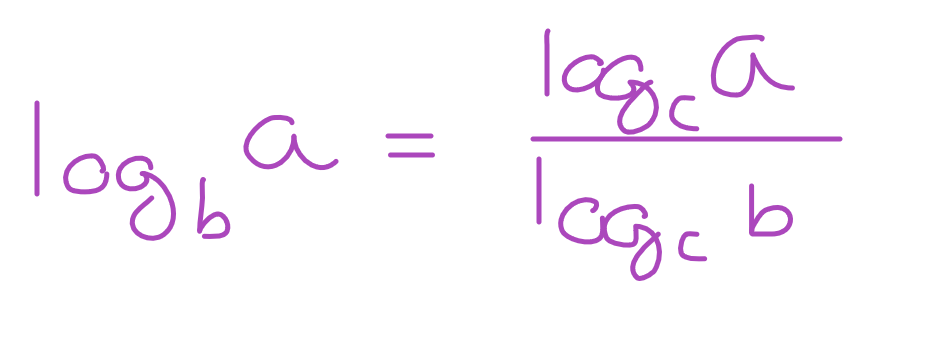
Now that we’ve reviewed the formula, let’s apply it to our initial problem – evaluating log7(5). The following is the step-by-step solution process.

Evaluating log₇(5)

Step 1: Rewrite the logarithm using the Change of Base Formula.

To aid us in rewriting the logarithm, we can determine the variables a, b, and c, and then plug these into the quotient form. Remember that c is the new base of the logarithms in the quotient and needs to be a base present on a calculator for this to prove effective.

Since a logarithm with base 10 is present, we’ll use 10 as c. Thus:

a = 5

b = 7

c = 10

Now, we can substitute these into the form:

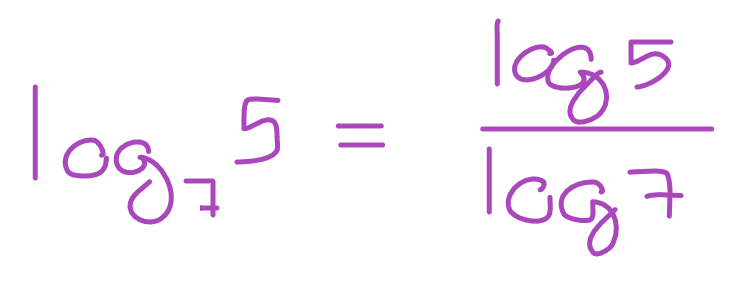
Step 2: Evaluate the resulting expression.

Now that we have an expression, we can use a calculator to evaluate it. 

For this demonstration, we’ll use the Desmos Scientific Calculator:

Step 3: Round.

All that’s remaining is to round. 

We’ll round to the nearest thousandth to get log7(5)  ≈ 0.827.

In summary, the key to evaluating any logarithm using the Change of Base Formula can be expressed in three steps:

1. Rewrite – use the Change of Base Formula to rewrite the logarithm using a base that is present on a calculator;
2. Evaluate – use a calculator to evaluate the quotient;
3. Round – round to the decimal place you are given in a problem.

Now that you know how to evaluate any logarithm, it’s time for you to become inducted into the world of logarithmic equations – but that’s for another lesson. For now, enjoy knowing that next time you’re presented with a problem like the one in the intro, you’ll know exactly what to do.