Worked Problems
Solving for Side Lengths with Trig Functions
Tip 1:
I highly recommend that you write down the SOH CAH TOA definitions while you work these problems. It will help you remember the trig functions, and can help you see how to break down complex problems into manageable calculations.
Problem #1
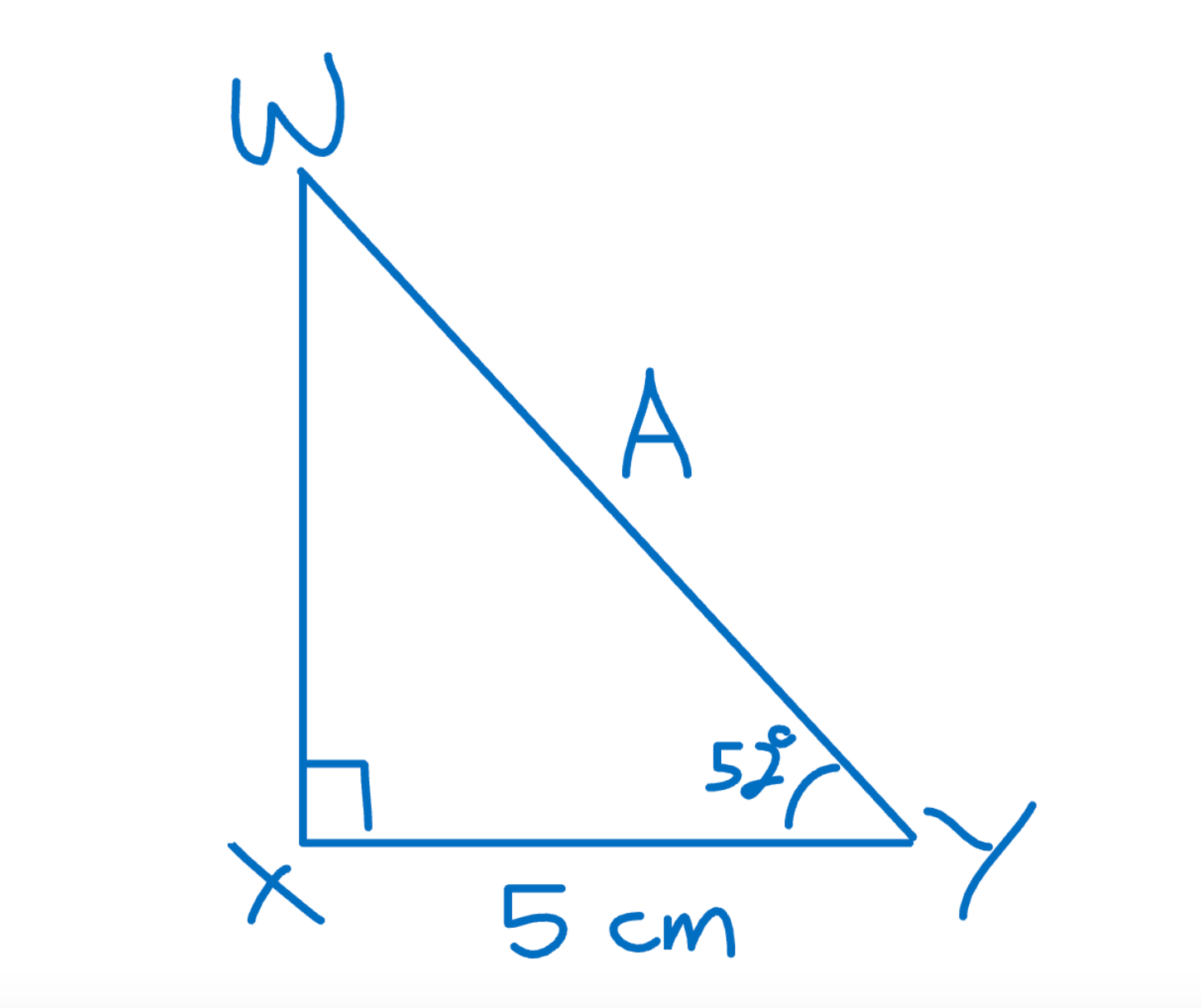
Solve for A (the length of segment WY) in the right triangle below. Round to the nearest tenth, if necessary.
How I Solve This
This is one of those problems in which I’m given an angle measure and a side length, and asked to solve for the length of another side. I usually solve these problems in four steps.
Step 1: Trig Function.
First, I determine what trigonometric function (sine, cosine, or tangent) relates the angle and side I do know to the side whose length I need to solve for. To do this, I consider how the two triangle sides are related to the angle I’m given. I will denote the angle as ∠WYX.
Segment XY, which is 5 cm long, is adjacent to ∠WYX. Segment WY can also be considered to be adjacent, but I know from the fact that it is opposite the right angle that it must be the hypotenuse – the longest side of the triangle. This means that I’m relating the adjacent side to the angle and the hypotenuse. The trigonometric function that deals with this is cosine, so I’ll use that to set up an equation to solve for A.
Step 2: Equation.
The length of segment XY is 5 cm, and the length of segment WY is A cm.
The cosine of ∠WYX can be expressed as follows:
cos(52˚) = 5/A
Now, I solve for A:
cos(52˚) = 5/A
cos(52˚) • A = 5
A = 5/cos(52˚)
Step 3: Solve.
I can plug the expression 5/cos(52˚) into my calculator to get the approximate answer for A.
As always, I make sure that my calculator is in degree mode, not radian mode (since I’m dealing with degrees).
From the calculator I find that:
A ≈ 8.121 ≈ 8.1
Step 4: Answer.
Rounded to the nearest tenth, the length of segment WY is 8.1 cm.
Extra Step (For A+ Students): Check.
I check my answer by finding the ratio of 5 to 8.1. It should approximate cos(52˚).
cos(52˚) ≈ 0.62
5/8.1 ≈ 0.62
I got the answer right.
Problem #2
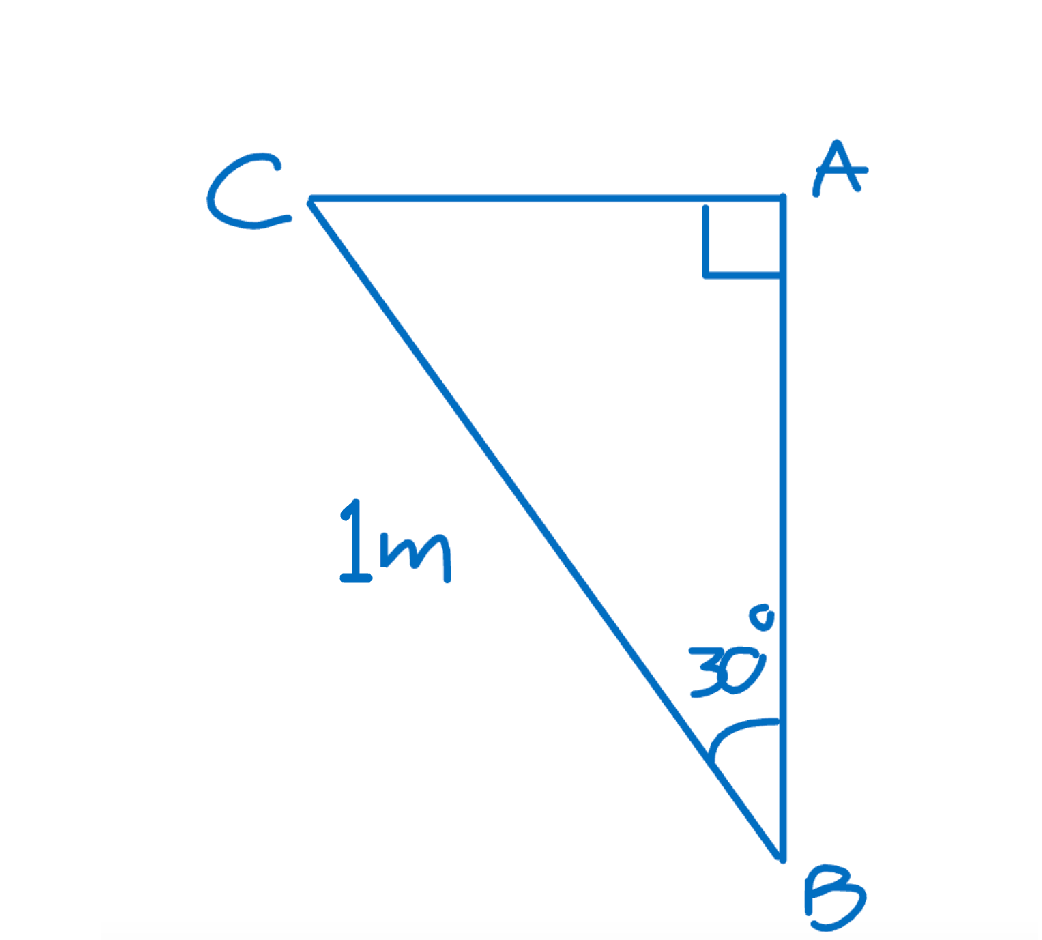
Given the triangle below, what is tan(∠ABC)?
How I Solve This
This is a two-part question. The first step is determining the sine and cosine of ∠ABC, and the second step is using those values to determine the tangent of ∠ABC. I solve this problem in four total steps.
Step 1: Side Lengths.
This particular triangle set-up doesn’t require me to use a calculator to solve for the sine and cosine of ∠ABC, because I recognize that this is a special 30-60-90 triangle.
Given that the length of the hypotenuse is 1 m, I can determine by the special side length ratios that the length of segment CA (opposite ∠ABC) is 1/2 m, or 0.5 m, and the length of segment AB (adjacent ∠ABC) is √3/2 m, which is about 0.87 m.
Step 2: Sine and Cosine.
Knowing the lengths for segments CA and AB makes it easy for me to now determine the sine and cosine of ∠ABC:
sin(∠ABC) = sin(30˚) = (½)/1 = ½
cos(∠ABC) = cos(30˚) = (√3/2)/1 = √3/2
Step 3: Tangent.
The tangent of a general angle is defined as:
tan(𝜃) = sin(𝜃)/cos(𝜃)
So for ∠ABC:
tan(∠ABC) = sin(∠ABC)/cos(∠ABC)
I know that sin(∠ABC) = ½ and cos(∠ABC) = √3/2, so the result becomes:
tan(∠ABC) = (1/2)/(√3/2) = 1/2 • 2/√3 = 1/√3 = √3/3
Step 4: Answer.
The tangent of ∠ABC is √3/3.
Extra Step (For A+ Students): Check.
I’ll check that tan(∠ABC) = √3/3 by evaluating tan(30˚) directly on my calculator (in degree mode) and comparing that to √3/3.
√3/3 ≈ 0.577
tan(30˚) ≈ 0.577 = √3/3
The results are actually equal to each other, so I got the answer right.
Summary of My Method
The two problems shown above are different in nature, so they require different problem-solving strategies. However, to find all side lengths with trig functions, I do follow some general steps:
- Determine the trig function – Using the information given, I determine which trig function will help me solve for the side length I need.
- Write the equation and solve – I write an equation using the information from Step 1 to solve for the missing side length. I then solve it by evaluating with a calculator. I make sure to round to the specified decimal place.
- Check – It’s always important to check the answer to make sure I used the correct trig ratio(s) and performed the calculation correctly. I also make sure that my calculator was in the correct mode when I did the calculation. Often, you’ll be given angles in degrees when solving for side lengths, so make sure the calculator is in degree mode and not radian mode.
If needed, I solve for multiple side lengths to solve the bigger problem.
If you have any questions or would like some help with problems like these, feel free to send me a message. I hope these calculations will help you as you continue on your journey of math mastery 🙂
~ Your Humble Study Buddy,
Ace
