Take a look at a calculator – a virtual one or a physical one. You’ll see keys you’re familiar with, such as π or a number key, but there are also some keys you probably won’t be familiar with. Specifically, have you ever noticed the sin, cos, and tan keys and wondered what they do?

In this post, you’ll find out.

Sin, cos, and tan are known as “trigonometric ratios.” They stand for “sine,” “cosine,” and “tangent,” respectively. So what are trigonometric ratios?

Simply put, they relate two specific sides of a right triangle and a specific angle in that right triangle. To explain what they are, let’s use a right triangle of our own.

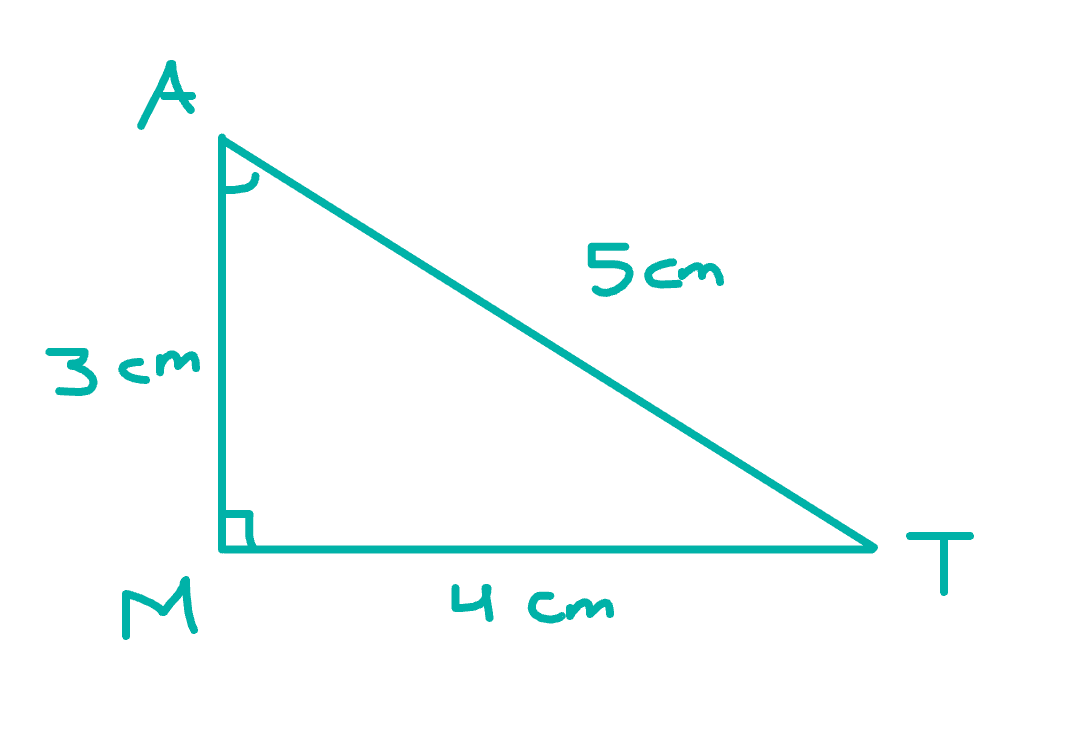
The triangle above is a right triangle (it has one right angle). A little bit of terminology to get out of the way before we delve into the trigonometric ratios:

• The hypotenuse of a right triangle is the longest side of the triangle. It is always opposite the right angle. In our case, the hypotenuse has a side length of 5 cm.
• The legs are the other two sides of the triangle.
• For a given specified angle (of which you are supposed to find the sin, cos, or tan value), the opposite side is the leg that is opposite the angle, and the adjacent side is the leg that is adjacent to the angle. In our triangle, relative to ∠MAT, the opposite side is 4 cm long and the adjacent side is 3 cm long.

Now that you know what “hypotenuse,” “adjacent,” and “opposite” refer to, let’s dive into the basic definitions of the trig functions. 

The sine function of a general angle, which we can represent with the symbol 𝜃 (“theta”), is defined as: sin(𝜃) = opposite/hypotenuse. This means that the sine of the angle is the ratio of the length of the triangle leg opposite the angle to the length of the hypotenuse. 

The definitions of cosine and tangent of 𝜃 are as follows:

cos(𝜃) = adjacent/hypotenuse

tan(𝜃) = opposite/adjacent

The hypotenuse refers to the length of the longest side of the triangle, and opposite and adjacent are the side lengths of the respective legs relative to 𝜃. 

To put this in more concrete terms, let’s find the sine, cosine, and tangent of an angle in our original right triangle above. Let’s say that 𝜃 = ∠MAT. What are the trig ratios for the angle?

First, let’s recap what we know about the specific sides:

> The hypotenuse is 5 cm.

> The adjacent leg is 3 cm.

> The opposite leg is 4 cm.

Now, let’s proceed to implement the definitions of sine, cosine, and tangent.

An easy way to remember the trig functions and their respective definitions is to use the acronym SOH CAH TOA.

Here’s how it works:

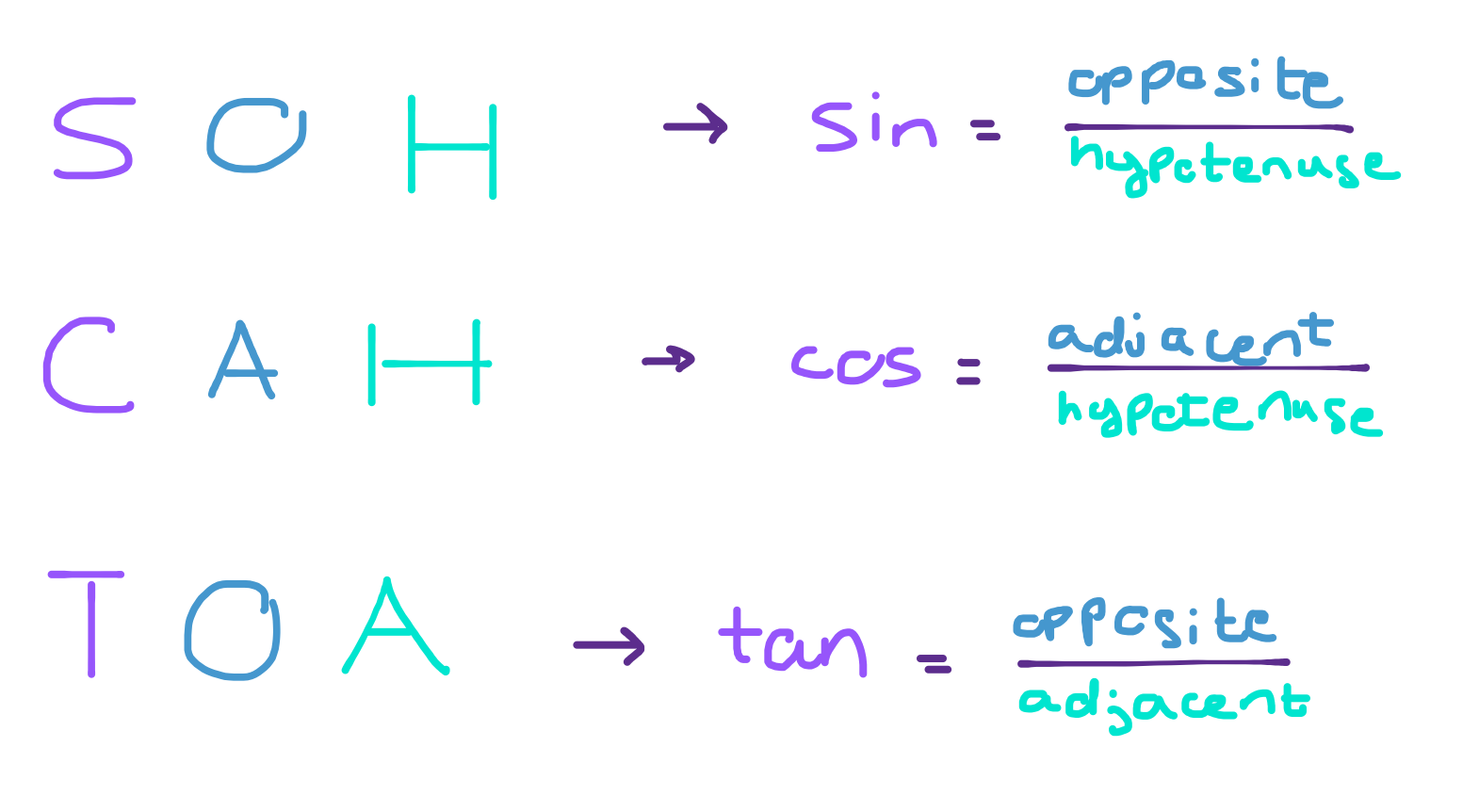
That’s a basic introduction to the trigonometric functions, and how you can apply them. But you’ll notice that we didn’t actually cover how to use the sin, cos, and tan keys on your calculator, or why they’re useful. Well, you’ll learn what they do as you progress to higher mathematics (Algebra 2 and beyond), but you’ll be able to see how you can use them to solve for angle measures and side lengths in right triangles in the next few posts.

So stay tuned!